
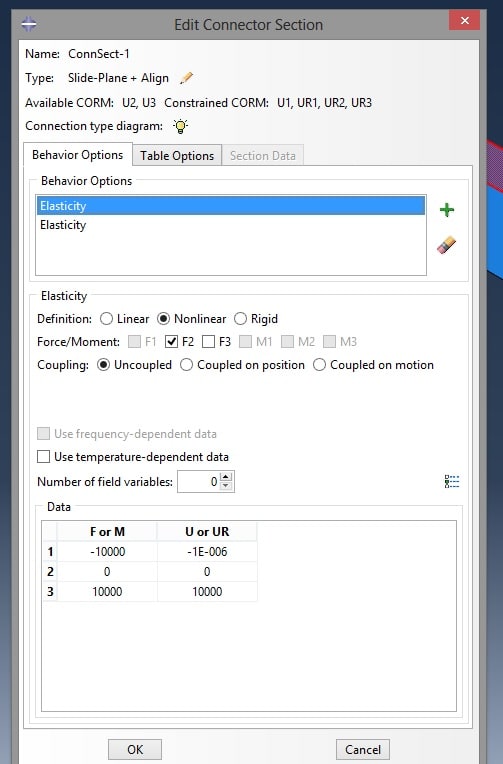
In both hybrid models, connectors for tensile behaviour are combined with membranes for consideration of the in-plane shear.
#Hypoelastic connectors abaqus 6.13 software
Two hybrid discrete continuous approaches based on mesoscale modelling are developed and implemented in the Abaqus software using VUMAT subroutines. 3 compares the analytical solutions (CASE 4) with the numerical ones, considering the fixed increment size as 0.In this study, the behaviour of woven composite fabrics under large deformation is investigated. Therefore, the hypoelastic constitutive equations based on the Kirchhoff stress tensor are equivalent to those based on the Cauchy stress tensor. \(J=1\)) and, thus, the Kirchhoff stress tensor coincides with the Cauchy stress tensor. In simple shear, the local volume does not change (i.e. 2 for the analytical solutions of the zero-graded hypoelastic constitutive equations under simple shear). Using the zero-graded hypoelastic constitutive equations in this model, the numerical Cauchy stress tensors can be checked with the analytical counterparts provided in (see Fig. This model is a displacement-based model subjected to simple shear. 1a), the nodes located on the bottom surface of the element are fixed in all directions, the nodes on the upper surface are fixed in \(x_2\) and \(x_3\) directions and a displacement equal to 5 is applied at the upper nodes in \(x_1\) direction. For automatic incrementation, the initial increment size is selected 100 times smaller than the maximum increment size and the minimum increment size is chosen 100 times smaller than the initial increment size.

For the force-based models, the incrementation type is set to automatic, and, for the displacement-based models, the fixed incrementation type is used. Next, the formulation behind such UMAT-subroutine variables as the consistent Jacobian ( \(\) step employs the Newton-Raphson method for the iteration. Next, the relations between the elasticity tensors of various hypoelastic models and the elasticity tensor relating the Jaumann rate of the Kirchhoff stress to the rate of deformation are constructed. The study starts with a review of some basic definitions, the concept of objective rate and the structure of hypoelastic constitutive models. , such relations seemed difficult to be constructed for models associated with the Green–Naghdi stress rates however, the kinematical relations provided in Mehrabadi and Nemat-Nasser enable us to establish such connections. To attain this, it is essential to express the elasticity tensor of the hypoelastic model in terms of the elasticity tensor which relates the Jaumann rate of the Kirchhoff stress tensor to the rate of deformation. This study aims to formulate and implement various hypoelastic constitutive models into the ABAQUS UMAT (user material) subroutine. We remark that the definition of elements in ABAQUS is based on the Jaumann rate for solid elements and on the Green–Naghdi rate for structural elements (shells, membranes, beams, trusses), as mentioned in the ABAQUS Theory Manual, Section 1.5.3. However, zero-graded hypoelastic models which are based on the Truesdell or Green–Naghdi rates do not suffer this problem. a hypoelastic model with constant isotropic elasticity tensor, exhibits oscillation in simple shear, if it is constructed based on the Jaumann rate of the Cauchy stress.

Originally, Dienes showed that the zero-graded hypoelastic model, i.e.
Hypoelasticity is a rate form of elastic material model, in which an objective stress rate is linearly related to the rate of deformation by means of a fourth-order elasticity tensor which, in general, is not obtainable from a strain energy density. The UMAT subroutine codes are provided in the “Electronic Supplementary Material” repository for the user’s consideration. The developed UMAT subroutine codes are validated using available solutions, and the consequence of using wrong Jacobian matrices is elucidated. This study aims to formulate and implement various hypoelastic constitutive models into the ABAQUS UMAT subroutine.
#Hypoelastic connectors abaqus 6.13 update
The user subroutine UMAT is the platform to implement a general constitutive model into ABAQUS, but, in order to update the Jacobian matrix DDSDDE in UMAT, the model must be expressed in terms of the Jaumann rate of the Kirchhoff stress tensor. The finite element analysis software ABAQUS uses a co-rotational frame which is based on the Jaumann rate for solid elements and on the Green–Naghdi rate for shell and membrane elements. The Truesdell, Jaumann, and Green–Naghdi rates of the Cauchy and Kirchhoff stress tensors are examples of the objective stress rates.
In hypoelastic constitutive models, an objective stress rate is related to the rate of deformation through an elasticity tensor.


 0 kommentar(er)
0 kommentar(er)
